定向耦合器的相矢图

相矢图

分析 2x2 定向耦合器的一个简单的方法是用所谓的正交模式法，参照 R. Youngquist, L. Stokes, and H. Shaw, “Effects of normal mode loss in dielectric waveguide directional couplers and interferometers,” IEEE J. Quantum Electron., Vol. 19, pp. 1888(1983).

这种方法认为耦合器中存在两个模式，一个是关于两个波导对称的（Even），另一个是关于两个波导反对称的（Odd）。这两个模式的相位差会随空间变化，通过控制耦合区长度来控制这个相位差即可控制耦合的分光比

现在固定对称模式的相位不动，让反对称模式的相位旋转，即可绘制出所谓的相矢图，如下所示。传输电场（输入光所在波导的输出电场，用下标 表示）是对称模式与反对称模式相加，耦合电场（用下标 表示）是对称模式减去反对称模式

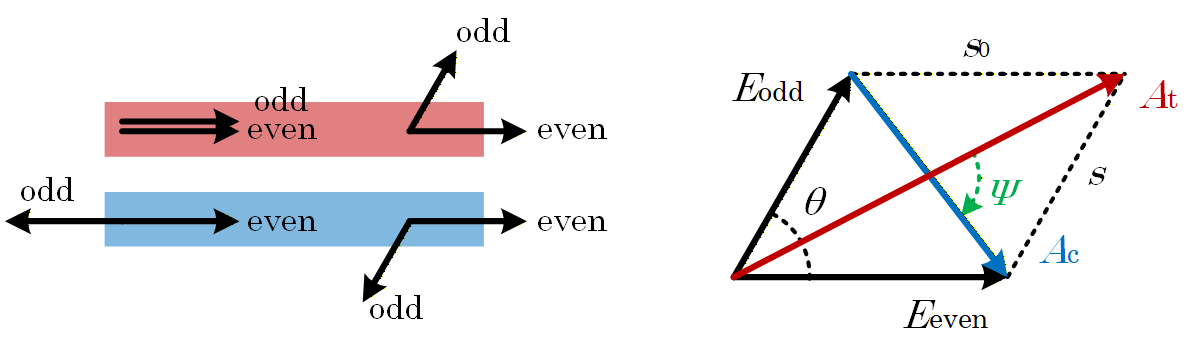
在理想情况下，两个模式之间没有差分损耗，那么不管是加还是减，两个模式的相矢总是张成菱形，而输出的总电场分别是菱形的两条对角线。由于菱形的性质，这两个输出电场之间总是存在着90°的相位差

将对称模式记为 ，非对称模式记为 ，那么两个输出总电场分别是

$$A_\mathrm{t} = s_0 + se^{j\theta} \quad,\quad A_\mathrm{c} = s_0 - se^{j\theta}$$

从而两个输出光强分别是

$$\begin{aligned} & I_\mathrm{t} = (s_0 + s\cos\theta)^2 + s^2\sin\theta = s_0^2 + s^2 + 2s_0 s\cos\theta \\ & I_\mathrm{c} = (s_0 - s\cos\theta)^2 + s^2\sin\theta = s_0^2 + s^2 - 2s_0 s\cos\theta \end{aligned}$$

两个输出电场之间的夹角 可以由下式计算出

$$\psi = \angle\left( \frac{A_\mathrm{c}}{A_\mathrm{t}} \right) \quad,\quad \frac{A_\mathrm{c}}{A_\mathrm{t}} = \frac{s_0^2 - s^2 - j2s_0s\sin\theta}{s_0^2 + s^2 + 2s_0 s\cos\theta}$$

在没有差分损耗，即 时，显然是一个纯虚值，那么 和 之间自然始终是正交的

与此同时，在输入时显然 ，且由于刚进入耦合器还没有损耗所以 ，因此输入光强

非理想误差

分析法

通过设计波导长度可以控制 ，但由于两个模式间存在差分损耗，以及温度可能带来耦合区长度的微变

记微小的差分损耗（的相反数，因为损耗一定表现为负值）为 ，非理想的角度漂移为 ，那么

$$\begin{aligned} & \mathrm{d}A_\mathrm{t} = \frac{\partial A_\mathrm{t}}{\partial s} \mathrm{d}s + \frac{\partial A_\mathrm{t}}{\partial \theta} \mathrm{d}\theta = e^{j\theta} \mathrm{d}s + js e^{j\theta} \mathrm{d}\theta \\[12pt] & \mathrm{d}A_\mathrm{c} = \frac{\partial A_\mathrm{c}}{\partial s} \mathrm{d}s + \frac{\partial A_\mathrm{c}}{\partial \theta} \mathrm{d}\theta = -e^{j\theta} \mathrm{d}s - js e^{j\theta} \mathrm{d}\theta \end{aligned}$$

而光强则是 ，代入即得到

$$\begin{aligned} \mathrm{d}I_\mathrm{t} &= (s_0 + se^{j\theta})(e^{-j\theta} \mathrm{d}s - js e^{-j\theta} \mathrm{d}\theta) + (s_0 + se^{-j\theta})(e^{j\theta} \mathrm{d}s + js e^{j\theta} \mathrm{d}\theta) \\ &= 2(s + s_0\cos\theta)\mathrm{d}s -2s_0 s\sin\theta \mathrm{d}\theta \end{aligned}$$

同样的做法得到

$$\begin{aligned} \mathrm{d}I_\mathrm{c} &= (s_0 - se^{j\theta})(-e^{-j\theta} \mathrm{d}s + js e^{-j\theta} \mathrm{d}\theta) + (s_0 - se^{-j\theta})(-e^{j\theta} \mathrm{d}s - js e^{j\theta} \mathrm{d}\theta) \\ &= 2(s - s_0\cos\theta)\mathrm{d}s +2s_0 s\sin\theta \mathrm{d}\theta \end{aligned}$$

在光学测量中，只有光强是可测的，所以上面两式是否构成可解的方程组尤为重要。将上面两式写为

$$\left[\begin{matrix} \mathrm{d}I_\mathrm{t} \\ \mathrm{d}I_\mathrm{c}\end{matrix}\right] = \left[\begin{matrix} 2(s+ s_0\cos\theta) & -2s_0 s\sin\theta \\ 2(s - s_0\cos\theta) & 2s_0 s\sin\theta \end{matrix}\right] \left[\begin{matrix} \mathrm{d}s \\ \mathrm{d}\theta \end{matrix}\right]$$

这个矩阵的行列式是

$$\det \left[\begin{matrix} 2(s+ s_0\cos\theta) & -2s_0 s\sin\theta \\ 2(s - s_0\cos\theta) & 2s_0 s\sin\theta \end{matrix}\right] = 8s_0s^2\sin\theta$$

这个行列式只有在 或 的时候为零，在其它偏置点处都不为零。因此除了两种特殊情况之外，矩阵总是可逆的，因而方程组总有唯一解

单独考虑特殊情况， 意味着反对称模式完全消失，那么耦合器已经失去功能了，这一般不太可能发生；而 意味着只有传输光波输出， 则是只有耦合光波输出

另一方面， 的微分是

$$\mathrm{d}\psi = \mathrm{d} \arctan\left( -\frac{2s_0 s \sin\theta}{s_0^2 - s^2} \right) = -\frac{(s_0^2 - s^2)\mathrm{d}(2s_0 s \sin\theta) - 2s_0 s \sin\theta \mathrm{d}(s_0^2 - s^2) }{(s_0^2 - s^2)^2 + 4s_0^2 s^2 \sin^2\theta}$$

分子上的微分分别是 和 ，代入得到

$$\mathrm{d}\psi = -\frac{[2s_0(s_0^2 - s^2)\sin\theta + 4s_0 s^2 \sin\theta ]\mathrm{d}s + 2s_0s(s_0^2 - s^2)\cos\theta\mathrm{d}\theta }{(s_0^2 - s^2)^2 + 4s_0^2 s^2 \sin^2\theta}$$

尤其值得考虑的是均等分光的情况，此时偏置点 ，那么

$$\begin{aligned} & \mathrm{d}A_\mathrm{t} = j \mathrm{d}s - s_0 \mathrm{d}\theta \\[12pt] & \mathrm{d}A_\mathrm{c} = j \mathrm{d}s + s_0 \mathrm{d}\theta \end{aligned}$$

由于电场强度难以测量，因此更有意义的是

$$\begin{aligned} & \mathrm{d}I_\mathrm{t} = 2s_0 \mathrm{d}s - 2s_0^2 \mathrm{d}\theta = \sqrt{I_0} \mathrm{d}s - \frac{I_0}{2} \mathrm{d}\theta \\[12pt] & \mathrm{d}I_\mathrm{c} = 2s_0 \mathrm{d}s + 2s_0^2 \mathrm{d}\theta = \sqrt{I_0} \mathrm{d}s + \frac{I_0}{2} \mathrm{d}\theta \end{aligned}$$

方程组中矩阵的行列式显然是 ，所以只要测量 和 即可得到差分损耗 和角度漂移 ，进而也就可以得到

$$\mathrm{d}\psi = -\frac{\mathrm{d}s}{s_0} = -\frac{2}{\sqrt{I_0}}\mathrm{d}s$$

作图法（均等分光）

对于均等分光的特殊情况，几何作图法也是有效的做法，并将导出完全一致的结果

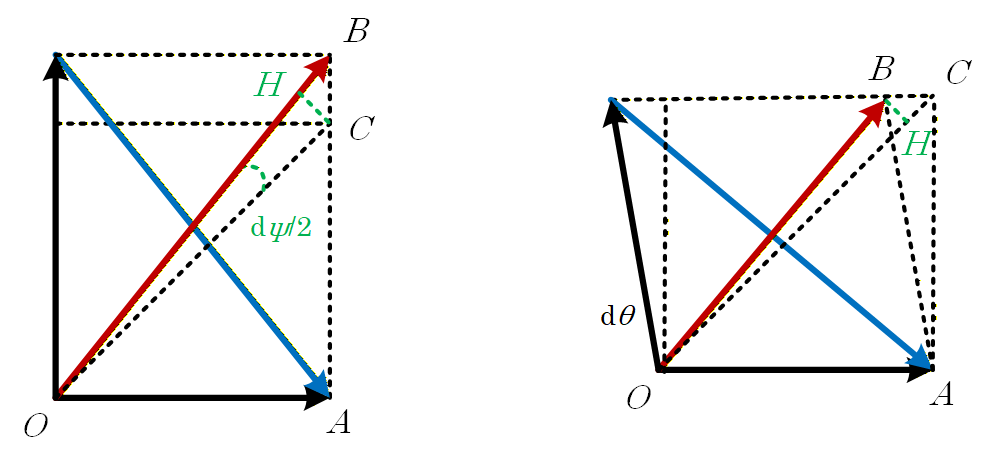
左图是存在差分损耗的情况，此时 是一个等腰直角三角形， ， ， ； 则是一个顶角无限小的等腰三角形（我的一位老师习惯称它为“直角等腰三角形”，这是因为 无限小，导致 都无限接近90° ）

是没有差分损耗时的 模长， 则是引入差分损耗后的模长，它们的差是

$$\mathrm{d}|A_\mathrm{t}| = OB - OC = OB-OH = BH = \frac{\mathrm{d}s}{\sqrt{2}}$$

对于 ，情况完全一致。偏置点满足 ，所以

$$\frac{\partial I_\mathrm{c}}{\partial s} = \frac{\partial I_\mathrm{t}}{\partial s} = \frac{2|A_\mathrm{t}|\mathrm{d}|A_\mathrm{t}|}{\mathrm{d}s} = 2s_0 = \sqrt{I_0}$$

与此同时， 显然是 ，所以

$$\mathrm{d}\psi = -2\frac{CH}{OC} = -2\frac{\mathrm{d}s}{2s_0} = -\frac{\mathrm{d}s}{s_0} = -\frac{2}{\sqrt{I_0}}\mathrm{d}s$$

右图则是存在角度漂移的情况，此时 也是一个等腰直角三角形， ， ； 是一个顶角无限小的等腰三角形

是没有角度漂移时的 模长， 则是引入角度漂移后的模长，它们的差是

$$\mathrm{d}|A_\mathrm{t}| = OB - OC = OH-OC = -CH = -\frac{s_0\mathrm{d}\theta}{\sqrt{2}}$$

对于 ，情况则完全相反。不过偏置点仍然是 ，所以

$$\begin{aligned} & \frac{\partial I_\mathrm{t}}{\partial \theta} = \frac{2|A_\mathrm{t}|\mathrm{d}|A_\mathrm{t}|}{\mathrm{d}\theta} = -2s_0^2 = -\frac{I_0}{2} \\[12pt] & \frac{\partial I_\mathrm{c}}{\partial \theta} = \frac{2|A_\mathrm{c}|\mathrm{d}|A_\mathrm{c}|}{\mathrm{d}\theta} = 2s_0^2 = \frac{I_0}{2} \end{aligned}$$

菱形的对角线始终垂直，因此角度漂移带来的 ，最终仍然得到

$$\left[\begin{matrix} \mathrm{d}I_\mathrm{t} \\ \mathrm{d}I_\mathrm{c}\end{matrix}\right] = \left[\begin{matrix} \sqrt{I_0} & -I_0/2 \\ \sqrt{I_0} & I_0/2 \end{matrix}\right] \left[\begin{matrix} \mathrm{d}s \\ \mathrm{d}\theta \end{matrix}\right] \quad,\quad \mathrm{d}\psi = -\frac{2}{\sqrt{I_0}}\mathrm{d}s$$