FPGA实现一个简单的数字锁相环

这两天刚好看到锁相环的内容，然后就在想用数字的方法写一个 PLL 。在网上和书上看到很多效果很好的设计，但是相对而言也比较复杂。于是就好奇能不能直接把书上模拟 PLL 的一些结构用数字的方式类比一下，然后用 verilog 写出来之后发现效果并不是很好，即使稳定之后，输出的信号频率也还会有小的变化，而不是完全和输入信号锁定。但是大致记录一下思路可能也还是可以的

实际上 FPGA 中一般都有丰富的 IP 核可供调用，利用它们能做出效果相当好的 PLL ，不过自己手撸一个可能相对而言能加深一下理解

电荷泵锁相环的结构

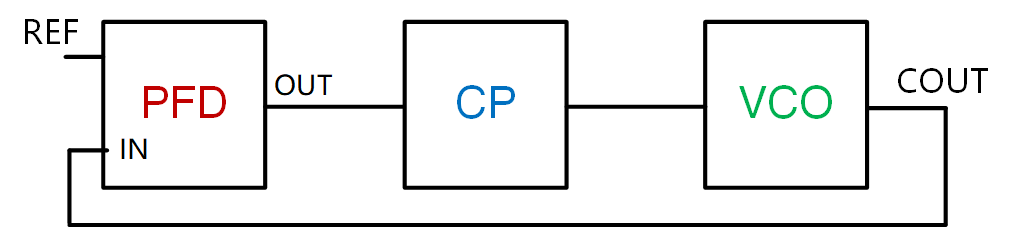
电荷泵锁相环（CPPLL）基本由三部分构成，包括鉴频鉴相器 PFD ，电荷泵 CP ，压控振荡器 VCO ，三者级联并最后将 VCO 的输出接到 PFD 的输入上构成反馈回路

鉴频鉴相器

PFD 有两个输入，一个输出。两个输入分别是参考的时钟信号和另一个输入的时钟信号，由于在 PLL 中 VCO 的输出接到 PFD ，所以这“另一个信号”实际上就是最终的输出时钟信号

构造 PFD 的第一步是构造鉴相器 PD ，将 PD 视为黑箱的话，它的输出是与两个输入时钟信号的相位差成正比的一个信号

$$f(\Delta \phi) = K\Delta \phi$$

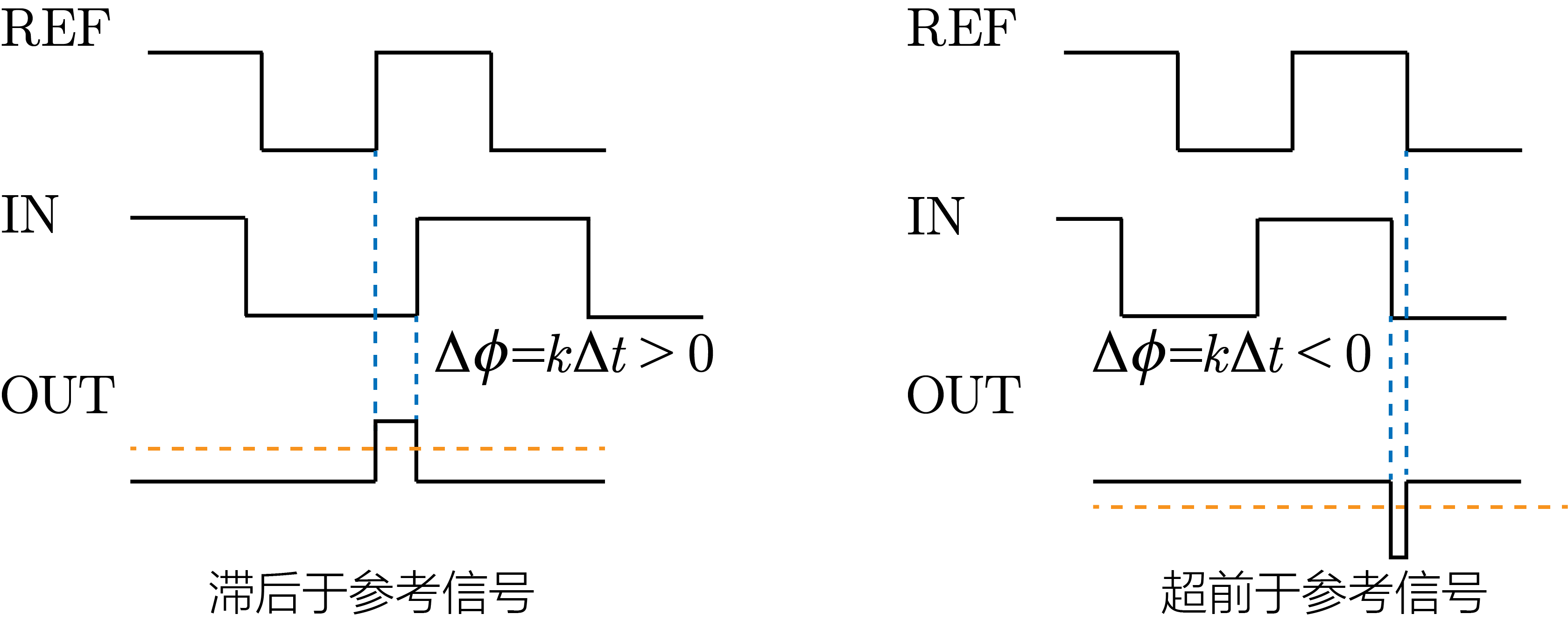
对于方波时钟信号相位差可以用两个信号的时钟沿之间的时间差来衡量，下图就分别就是输入信号的相位超前于参考信号和滞后于参考信号的情况

PD 的问题在于，如果参考信号和输入信号之间的频率相差过大就无法使锁相环正常工作，因而需要同时检测频率差和相位差，即构造 PFD ，PFD 的波形大概如下图。它的工作方式是

• OUT 可以取 0，1，-1 三个值

• 每当 REF 的上升沿到达时，就对 OUT 加 1 ；而当 IN 的上升沿到达时，则对 OUT 减 1

• 当 OUT 已经为 1 时，再加 1 的话 OUT 还是 1 ；当 OUT 已经为 -1 时，再减 1 的话 OUT 还是 -1

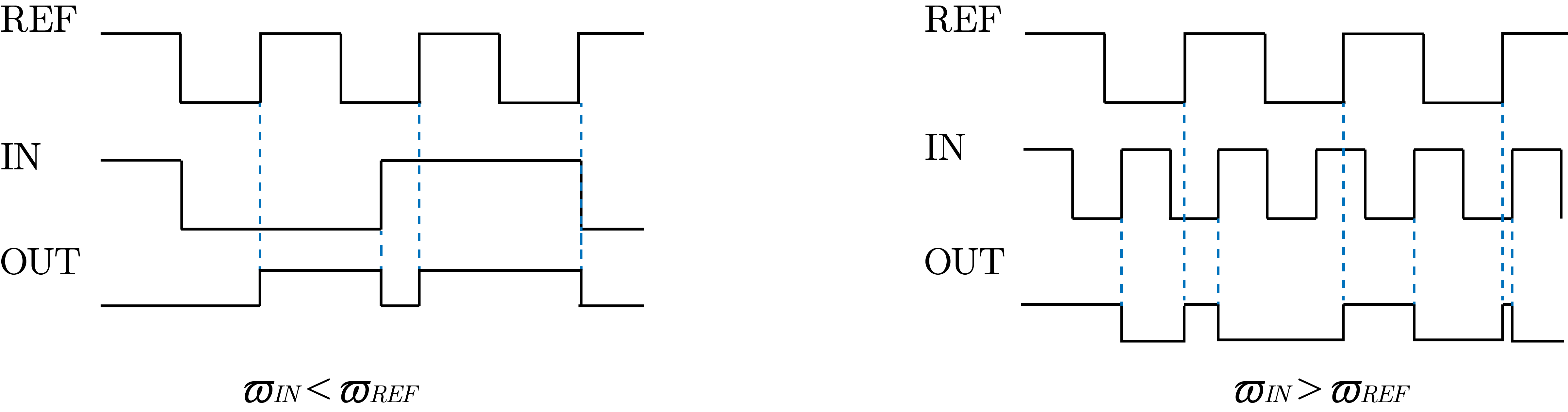
这样做的话，从波形中可以看出来如果 ，那么 OUT 将只在 1 和 0 之间变化，它的均值（即直流分量）总是大于 0 的；相反地，如果 ​ ，OUT 将只在 -1 和 0 之间变化，直流分量总是小于 0 的

锁相环最终的目的是令 IN 的频率等于 REF 的频率，所以有了 OUT 之后，还需要电荷泵提取出它的直流分量，然后将这直流分量输入进压控振荡器中，调整振荡器的频率，使得振荡器产生的信号（即这里的 IN ）频率与 REF 相等

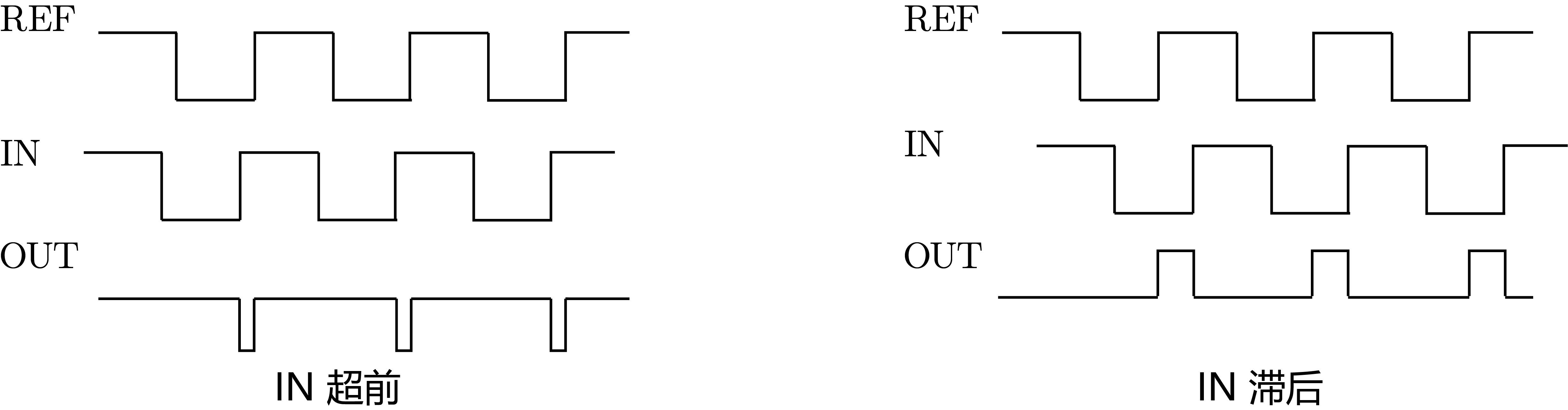
而如果 REF 和 IN 的频率相同但是相位不同，那么也将会如下图，每隔一个周期产生一个同方向的脉冲信号。因而 PFD 既能感知频率差，也能感知相位差，并且对于相同的关系其直流分量总是朝着一个方向的（比如当 时输出直流分量总是正的，当 滞后于 ​ 时输出的直流分量也总是正的）

电荷泵

电荷泵由一个电容构成，向电容充电可以提高极板上的电平，而令电容放电则可以降低极板上的电平。假定后面的压控振荡器其输出频率随输入电压的升高而增大，那么

• 当 的时候就应该给电容充电使电平升高，IN 的频率也升高
• 当 ​ 的时候则应该令其放电使电平降低，IN 的频率也降低

---

这个做法对频率相同而相位不同的信号也是适用的：

• 当 IN 超前时，电容会放电，使电平降低，从而 IN 频率降低；直到频率到某个足够高的值，使得 IN 的相位又开始滞后，电容又充电使 IN 频率升高，如此往复会令 IN 收敛于 REF
• 当 IN 滞后时，电容会充电，使电平升高，从而 IN 频率升高；直到频率到某个足够低的值，使得 IN 的相位又开始超前，电容又放电使 IN 频率降低，如此往复会令 IN 收敛于 REF

---

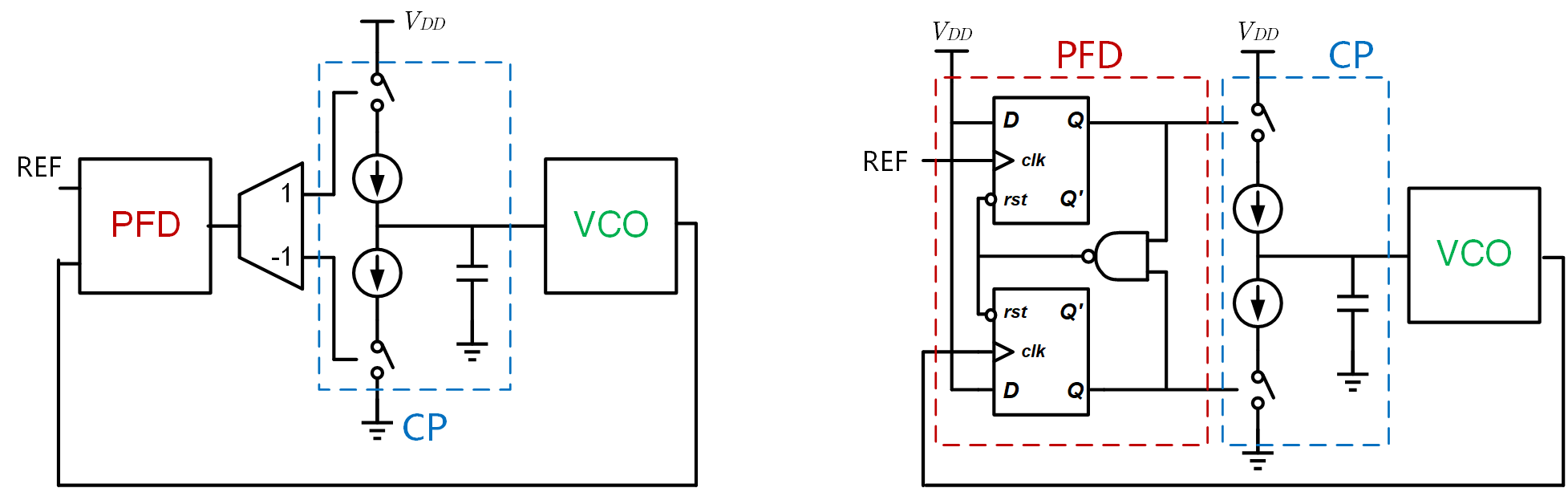
这样的话，也就是每当 OUT 为 1 的时候打开一个开关将电容和一个接到 VDD 的电流源相连，这样就会给电容充电；而每当 OUT 为 -1 的时候打开另一个开关，将电容和一个接到 GND 的电流源相连，就会令电容放电

所以就得到下图左侧的结构。右侧是 PFD 的一个具体实现，上面的 D 触发器一旦为 1 就打开上面的开关（相当于 OUT 为 1 ），而下面的 D 触发器一旦为 1 就打开下面的开关（相当于 OUT 为 -1 ），而一旦这两个触发器同时为 1 时，就立刻激活异步复位端，将两个 D 触发器都置为 0 ，从而关闭开关

压控振荡器

压控振荡器可以用环形振荡器或者 LC 振荡器实现。这里以环形振荡器为例，用 3 个反相器构成的回路产生正弦波动，再通过两个反相器可以将正弦波转变为类似方波的形式（这是因为只要输入电平升高到 而不是 ，输出电平就为 0；同样输入电平只要降低到 而非 0 ，输出电平就为 ​，进行两次这样的操作，正弦波的边缘就会变得比较陡峭，从而接近方波）

而环形振荡器的频率可以通过控制产生正弦波的三个反相器的电流实现，定性来看是因为改变电流会导致 改变，从而导致每个结点对应的时间常数改变。最终电路会成为

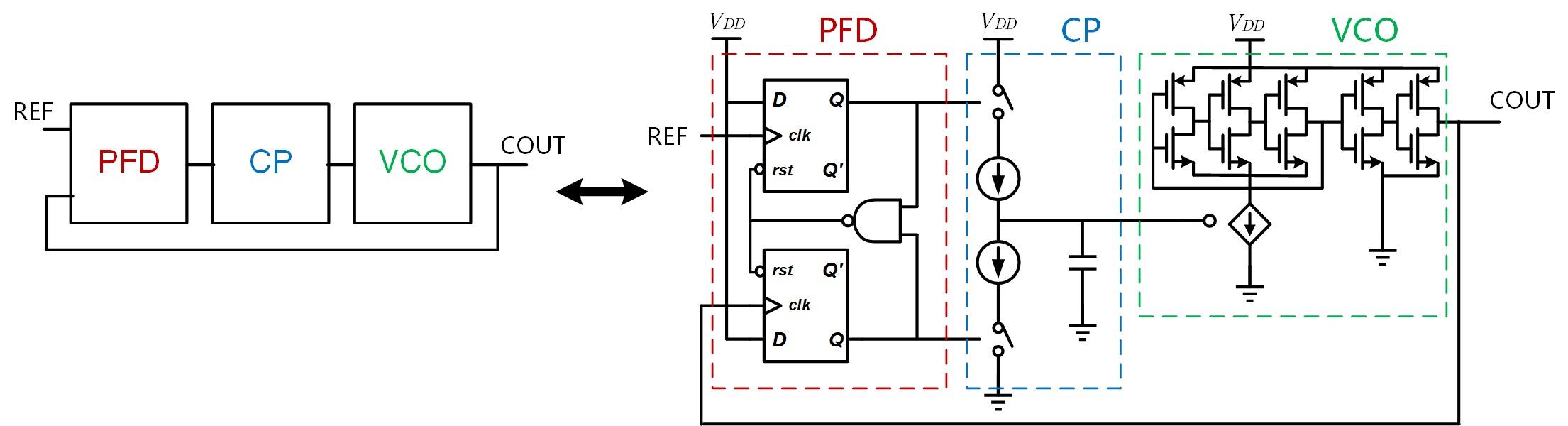
完整的 PLL 工作原理应当是 PFD 检测输出信号和参考时钟 REF 之间的频率与相位差，然后调节 CP 的电平，CP 的电平再作为 VCO 的控制电压修正输出信号的频率，以达到锁相的目的

数控振荡器

在 CPPLL 中 PFD 本来就是数字的，而 CP 和 VCO 是模拟的，也就是要想办法类比出“数字的 CP 和 VCO”

先从 VCO 开始，在数字系统中改变时钟频率最常用的方式就是利用计数器进行分频，所以 VCO 可以类比为计数器和 FPGA 上全局时钟的结合，控制电压则类比为计数器的计数上限

具体思路是这样的。创建一个计数器接入全局时钟，“数字 CP”确定一个计数上限 ，每当时钟上升边沿到来时，计数器加 1 ；直到某次时钟上升边沿到来时，计数器大于或等于 ，此时计数器归零，同时令输出信号反转。用 verilog 表达即是

input clk, areset;
input [3:0] uplimit;
output reg cout;
reg [3:0] counter;

always @(posedge clk, negedge areset) begin
    if(!areset) begin
        counter <= 0;
        cout <= 1;
    end
    else if(counter==uplimit || counter>uplimit) begin
        counter <= 0;
        cout <= ~cout;
    end
    else counter <= counter + 4'b0001;
end

比如令 （就是上面的 uplimit ），那么会有下图所示的输出波形。第一行是全局时钟，周期是 10 ，第二行是计数器，第三行是输出波形，周期是 80 ，也就是实现了 ​ 倍分频

可以通过改变 来改变输出周期，每当 增加 1 时，输出波形的周期增加 ，这里 是全局时钟的周期。 可以取到 0，但即使 取到 0 ，最小的输出周期也达不到全局时钟周期本身，而只能是全局时钟的 2 倍。此外 一旦改变至少会引起周期变化 ，也就是周期无法连续变化

电荷泵的数字类比

电荷泵的数字类比则是累加器，因为电荷泵的作用就是通过累积电荷来改变 VCO 的控制电压

具体的做法是构建一个寄存器，位数和数控振荡器的计数器位数相同，也接入全局时钟，并将寄存器的输出接入数控振荡器的 uplimit 。然后

• 每当检测到 PFD 中接 REF 的触发器变为 1 时，就令寄存器中的数减 1 ，从而减小数控振荡器输出的周期，即提高其频率
• 每当检测到 PFD 中接 COUT 的触发器变为 1 时，就令寄存器中的数加 1 ，从而增加数控振荡器输出的周期，即降低其频率

数字锁相环的实现

最终，将鉴频鉴相器，数字“电荷泵”，数控振荡器分别用 verilog 写出来就是

1. 鉴频鉴相器：low ，fast 分别是两个 D 触发器的输出

   module dpd(sig_ref, sig_in, areset, low, fast);
   	input sig_ref, sig_in, areset;
   	output reg low, fast;
   	wire rst;
   	
   	always @(posedge sig_ref, negedge rst) begin
   		if(!rst) fast <= 0;
   		else fast <= 1;
   	end
   	always @(posedge sig_in, negedge rst) begin
   		if(!rst) low <= 0;
   		else low <= 1;
   	end
   	assign rst = ~(fast & low) & areset;
   endmodule

2. 数字“电荷泵”：每当异步复位时，设定“初始计数上限”为 0x80 ，比较靠近 8 位数字的中心

   module dlpf(clk, areset, low, fast, uplimit);
   	input clk, areset, low, fast;
   	output reg [7:0] uplimit;
   	
   	always @(posedge clk, negedge areset) begin
           if(!areset) uplimit <= 8'h80;
   		else if(uplimit==8'h00) begin
   			if(low) uplimit <= uplimit + 8'h01;
   			else;
   		end
   		else if(uplimit==8'hFF) begin
   			if(fast) uplimit <= uplimit - 8'h01;
   			else;
   		end
   		else begin
   			case({low,fast})
   				2'b10: uplimit <= uplimit + 8'h01;
   				2'b01: uplimit <= uplimit - 8'h01;
   				default;
   			endcase
   		end
   	end
   endmodule

3. 数控振荡器

   module dco(clk, areset, uplimit, cout);
   	input clk, areset;
   	input [7:0] uplimit;
   	output reg cout;
   	reg [7:0] counter;
   	
   	always @(posedge clk, negedge areset) begin
   		if(!areset) begin
   			counter <= 8'h00;
   			cout <= 1;
   		end
   		else if(counter==uplimit || counter>uplimit) begin
   			counter <= 8'h00;
   			cout <= ~cout;
   		end
   		else counter <= counter + 8'h01;
   	end
   endmodule

然后用一个顶层模块将这三者实例化并相接

module top_module(sig_ref, areset, clk, sig_out);
	input sig_ref, areset, clk;
	output sig_out;
	wire fast, low;
	wire [7:0] uplimit;
	dpd D1(sig_ref, sig_out, areset, low, fast);
	dlpf D3(clk, areset, low, fast, uplimit);
	dco D2(clk, areset, uplimit, sig_out);
endmodule

RTL 综合后的电路模块图是

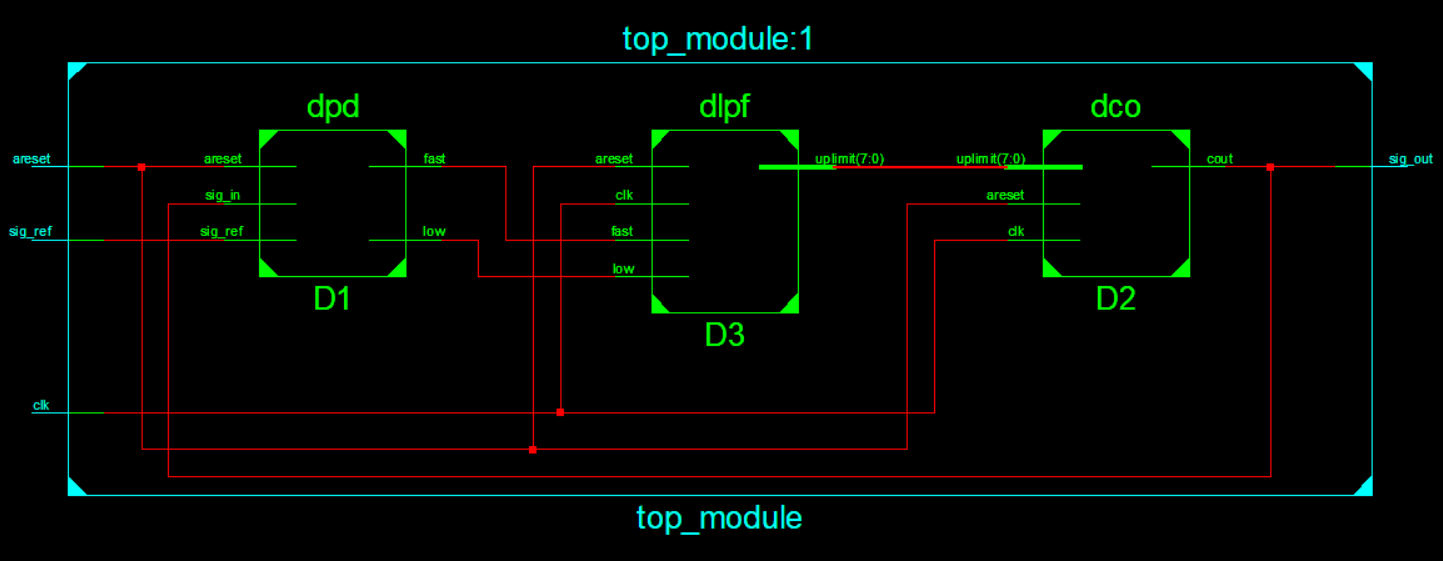
写出 testbench 进行仿真，设定输入的 REF 周期是全局时钟 clk 的 15 倍，结果如下（若以 Xilinx AX309 为例，其全局时钟是 ，那么 REF 就是 左右，横轴单位是 ）

可以看到一开始输出信号频率远低于 REF ，然后经数字 PLL 纠正，到 6~12 这段已经差不多稳定了，输出频率也很接近 REF 的频率。但是输出波形并没有完全锁定为 REF 的波形，方波有时略宽或略窄，fast 和 low 也都有小的脉冲

可以想来，如果是用理想的电荷泵进行积分的话，这种小脉冲会逐渐消失，最后输出完全和 REF 锁定。但是因为上面只是基于对 CPPLL 的类比，作为练习手撸的 PLL ，没有任何优化之类的，好像暂时也只能到这个地步