MOS和BJT的端口电阻

这里所说的 MOS 端口电阻是在低频情况下从漏端或者源端看进去的小信号电阻，即下图中的 ​ ；因为低频下一般认为从栅极看进去的电阻就是无穷大，所以没必要特意计算

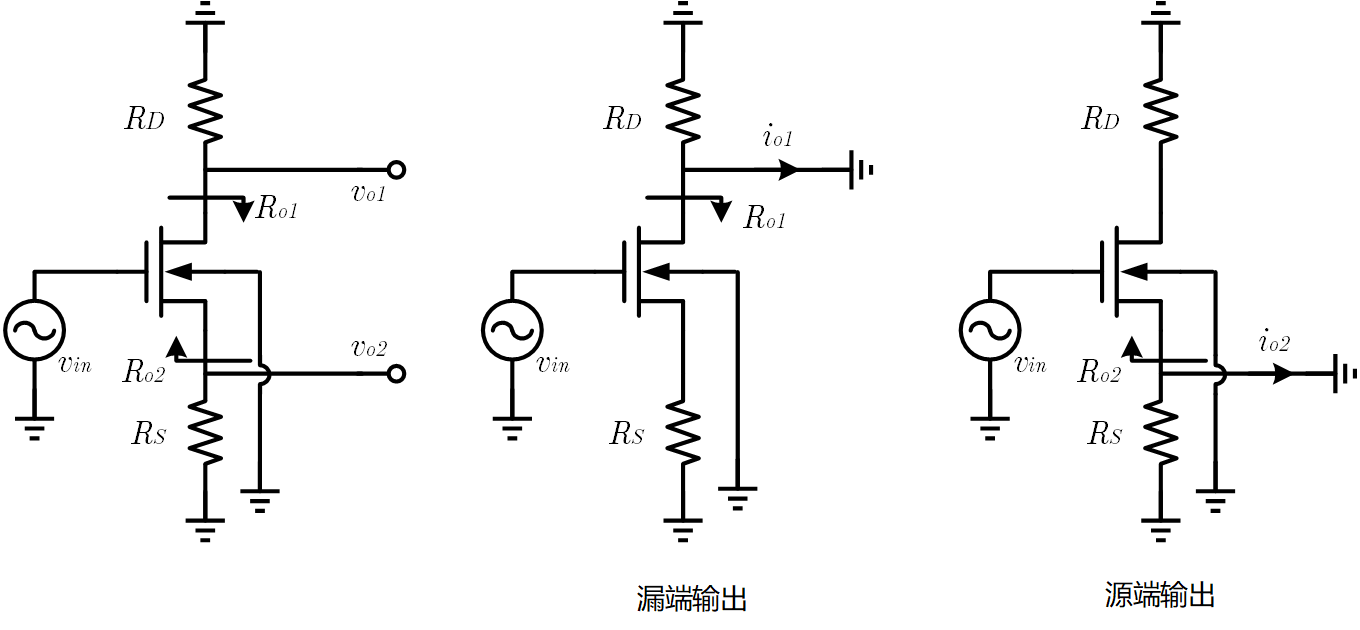
同时，也可以算出漏端输出和源端输出两种情况下的小信号跨导，即 和 的关系，从而可以直接利用 Norton 定理得出小信号电压增益。而通过将图中的 ​ 置零恰可以分别得到共源级和源极跟随器

而且这些结果表现出相当统一的形式，可以直接记住拿来用。尽管分析是对 NMOS 进行的，但是结论对 PMOS 也是适用的，因为二者结构是对称的

MOS 漏端输出

对于漏端输出的情况，计算小信号跨导和小信号输出电阻的小信号电路分别如下图

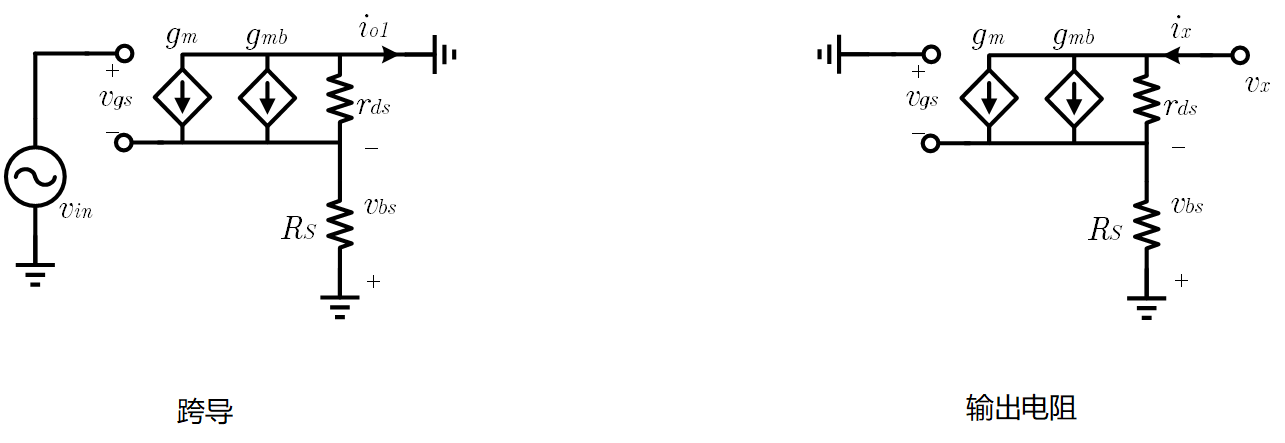
跨导增益

对计算跨导的小信号电路列写 KCL, KVL 得到

$$\begin{cases} v_{in} = v_{gs}-v_{bs} \\ i_{o1} = -g_{m}v_{gs} - g_{mb} v_{bs} - g_{ds}v_{bs} \\ v_{bs} = i_{o1} R_S \end{cases}$$

式中的 ，将第三式代入第一式，得到 ，再将该式和第三式代入第二式就有

$$i_{o1} = -g_mv_{in} - i_{o1}g_mR_S - i_{o1}g_{mb}R_S - i_{o1}g_{ds}R_S$$

整理可以得到

$$G_1 = \frac{i_{o1}}{v_{in}} = \frac{-g_m}{1+(g_{m}+g_{mb}+g_{ds})R_S}$$

输出电阻

对计算输出电阻的小信号电路列写 KCL, KVL 得到

$$\begin{cases} v_{gs} = v_{bs} \\ i_{x} = g_{m}v_{gs} + g_{mb} v_{bs} + g_{ds}(v_x + v_{bs}) \\ v_{bs} = -i_{x} R_S \end{cases}$$

将第三式代入第一式，得到 ，将该式和第三式代入第二式就有

$$i_x = -i_xg_mR_S - i_{x}g_{mb}R_S - g_{ds}(v_x-i_xR_S)$$

整理可以得到

$$R_{o1} = \frac{v_x}{i_x} = \frac{1+(g_m+g_{mb}+g_{ds})R_S}{g_{ds}} = [1+(g_m+g_{mb}+g_{ds})R_S]r_{ds}$$

这个倍乘系数（或者视为一个负反馈的环路增益）和上面跨导增益处是一样的，可以先记为 ，下面的源端输出也会给出类似的系数

MOS 源端输出

对于源端输出的情况，计算小信号跨导和小信号输出电阻的小信号电路则分别如下图

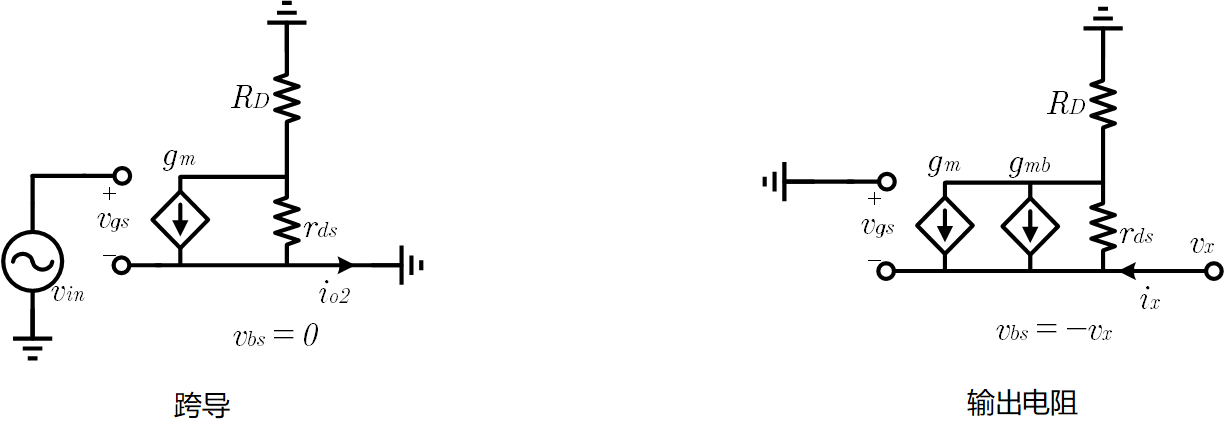
跨导增益

同样地，直接对计算跨导的小信号电路列写 KCL, KVL 得到

$$\begin{cases} v_{in} = v_{gs} \\ i_{o2} = g_{m}v_{gs} + g_{ds}v_d \\ v_{d} = -i_{o2} R_D \end{cases}$$

这里 指漏极的电压，将第三式和第一式代入第二式有

$$i_{o2} = g_mv_{in} - i_{o2}g_{ds}R_D$$

整理可以得到

$$G_2 = \frac{i_{o2}}{v_{in}} = \frac{g_m}{1+g_{ds}R_D}$$

输出电阻

还是直接对计算输出电阻的小信号电路列写 KCL, KVL 得到

$$\begin{cases} v_{gs} = v_{bs} = -v_x \\ i_{x} = -g_{m}v_{gs} - g_{mb} v_{bs} + g_{ds}(v_x -v_d) \\ v_{d} = i_{x} R_D \end{cases}$$

将第一式和第三式代入第二式就有

$$i_x = g_{m}v_x + g_{mb}v_x + g_{ds}(v_x - i_xR_D)$$

整理可以得到

$$R_{o2} = \frac{v_x}{i_x} = \frac{1+g_{ds}R_D}{g_m + g_{mb}+g_{ds}} = [1+g_{ds}R_D](1/g_m\ ||\ 1/g_{mb}\ ||\ r_{ds})$$

这个倍乘系数记为

MOS 情况的总结

由上面的内容，可以分别计算从漏端和源端输出时的电压增益，这只需要将跨导增益和输出电阻相乘即可，但是此时的输出电阻不止有 ，也有 ，即

$$A_{v1} = G_1 (R_{o1}\ ||\ R_D) = \frac{-g_m}{1+H_S} \cdot \frac{(1+H_S)r_{ds}R_D}{(1+H_S)r_{ds} + R_D} = \frac{-g_mR_D}{1+H_S + g_{ds}R_D}$$

以及

$$A_{v2} = G_2 (R_{o2}\ ||\ R_S) = \frac{g_m}{1+H_D} \cdot \frac{[(1+H_D)/(g_{m} + g_{mb}+ g_{ds})]R_S}{(1+H_D)/(g_{m} + g_{mb}+ g_{ds}) + R_S} = \frac{g_mR_D}{1+H_D + (g_{m} + g_{mb}+ g_{ds})R_S}$$

再注意到 和 就可以列出

• 漏端输出时：跨导增益 ；输出电阻 ；电压增益
• 源端输出时：跨导增益 ；输出电阻 ；电压增益

而由于很多情况下可以近似认为 ​ ，所以也可以利用上述关系快速判断端口阻抗是比较大还是比较小

应用到单级放大器上

1. 共源级

   令 即可，此时

   所以 ； ，是个大电阻； ，由于 相对较小，所以电压增益相对比较可观

2. 共漏级

   令 即可，此时 ​

   所以 ； ，是个小电阻； ，由于 相对较大，所以电压增益较接近但略小于 1

3. 共栅级

   共栅级稍微特殊一点，因为输入不在栅极。但是注意到输入在源端，而栅极接交流地，所以

   于是跨导可以直接写出为 ；输入电阻是从源极看进去的电阻 ，是个小电阻；输出电阻则为从漏极看进去的电阻 ，是个大电阻；电压增益为

BJT 的端口电阻

BJT 的混合 pi 模型和 MOS 的模型比较相似，只是多了一个 ，为基极电流提供了一个通路，所以可能会有相似的结论

从集电极输出

从集电极输出的情况如下图所示，右侧是小信号电路，其中

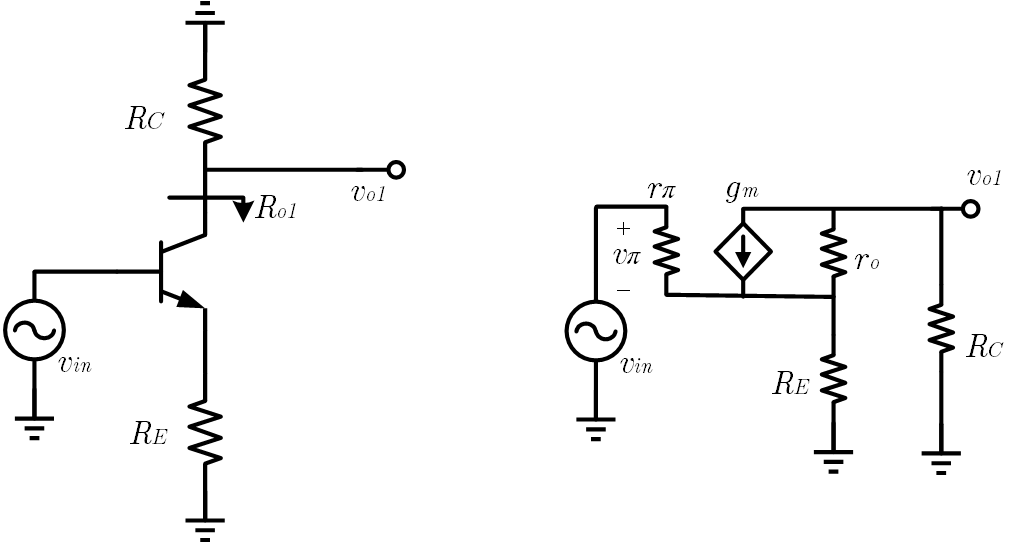
要计算 ，将 置零，然后从 的左边看进去。之后只要将 视为 ，其实就和 MOS 一样了，所以就有

$$R_{o1} = [1+(g_m+1/r_o)(r_{\pi}\ ||\ R_E)]r_o$$

从射极输出

从射极输出的情况如下图所示，右侧是小信号电路

要计算 ，将 置零，然后从 的左边看进去。如果 是开路，那么就和 MOS 一样了，而 又是并联在输出端口和交流地之间的，也就是说 相当于 MOS 的情况并上一个 ，即

$$R_{o1} = [1+R_E/r_o](1/g_{m}\ ||\ r_o)\ ||\ r_{\pi}$$

基极端口电阻

不同于 MOS ，即使在低频情况下，BJT 从基极看进去时也并不能视为开路。对于上面两种情况来说，从基极看进去的电阻都是一样的，如果先忽略 ，那么输入的电流就是 ，它流过 之后，被放大了 倍又流过 到交流地，所以

$$R_i = \frac{v_{in}}{i_b} = r_{\pi} + (\beta+1)R_E$$